The Scaling Laws of Human Travel
The goal of this project was to assess the statistical properties of human traffic on length scales of a few to a few thousand kilometers. A very simple question that initially motivated this was “What is the probability of a human being travelling a certain distance in a short period of time?” taking into account all possible means of transportation. Simple as it is, this question is difficult to answer because in order to do so one would have to collect and compile date for various involved human traffic networks: air transportation, highway traffic as well as railroad networks.
Movie 1: The scaling laws
of human travel: Television Feature on DW-TV. (Click on
image to watch.)
In this project we approached the problem from an unusual angle. Instead measuring the geographical movement of individuals, we evaluated data collected at the online bill tracking system www.wheresgeorge.com in order to assess the statistical properties of the geographic circulation of money instead. The idea behind this project was to use the dispersal of money as a proxy for human travel as bank notes are primarily transported from one place to another by traveling humans.
Wheresgeorge.com, which was invented by Hank Eskin in 1998, is a popular US internet game in which participants can register individual dollar bills for fun and monitor their geographic circulation. Since its beginning a vast amount of data has been collected at the website, over 100 millions of dollar bills have been registered by over 3 million registered users and over 10 million bills have had "hits", that means they resurfaced somewhere else.
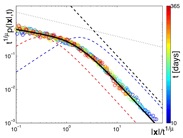
Our initial study was based on a dataset of roughly a million individual displacements. We found that the dispersal of dollar bills can be described by a set of simple mathematical laws. First, the probability of traveling a distance in a short period of time days decays as a power law, i.e.
This observation lead us to conjecture that the trajectories of dollar bills are reminiscent of Lévy flights, superdiffusive random walks characterized by a power law in the single step distribution.
The situation turned out to be more complex, as also broadly distributed waiting time distributions play a role which leads to a subdiffusive component of money dispersal and a competition of long jumps and long waiting times. Effectively money dispersal can be described with a bi-fractional diffusion equation.